רדיוס התכנסות
במתמטיקה, רדיוס ההתכנסות של טור חזקות הוא רדיוס הדיסק הגדול ביותר במרכז הסדרה בה מתכנסת הסדרה. זה מספר ממשי לא שלילי או . כשהיא חיובית, סדרת החזקה מתכנסת באופן מוחלט ואחיד על קבוצה קומפקטית בתוך הדיסק הפתוחה ברדיוס השווה לרדיוס ההתכנסות, וזוהי סדרת טיילור של הפונקציה האנליטית שאליה היא מתכנסת. במקרה של ריבוי סינגולריות של פונקציה (סינגולריות הם ערכים של הארגומנט שעבורם הפונקציה לא מוגדרת), רדיוס ההתכנסות הוא המינימלי מכל המרחקים המתאימים (שכולם מספרים לא שליליים) המחושבים מתוך מרכז דיסק ההתכנסות לסינגולריות המתאימות של הפונקציה.
הַגדָרָה[עריכת קוד מקור | עריכה]
עבור סדרת חזקות f המוגדרת כ:
על הגבול, כלומר עבור , ההתנהגות של סדרת החזקה עשויה להיות מסובכת, והסדרה עשויה להתכנס עבור כמה ערכים של z ולהתבדר עבור אחרים. רדיוס ההתכנסות הוא אינסופי אם הסדרה מתכנסת עבור כל המספרים המרוכבים z . [1]
רדיוס ההתכנסות r הוא מספר ממשי לא שלילי או כך שהסדרה מתכנסת אם
ומתבדרת אם
אחרים עשויים להעדיף הגדרה חלופית, שכן הקיום ברור:
כאשר
מציאת רדיוס ההתכנסות[עריכת קוד מקור | עריכה]
קיימים שני מקרים. המקרה הראשון הוא תיאורטי: כאשר יודעים את כל המקדמים , עבור הגבולות הידועים מוצאים את רדיוס ההתכנסות המדויק. המקרה השני הוא מעשי: כאשר בונים פתרון עבור סדרת חזקה של בעיה קשה, בדרך כלל נדע רק מספר סופי של מונחים בסדרת חזקה, בכל מקום מכמה איברים עד מאה איברים. במקרה השני הזה, אקסטרפולציה של גרף מעריכה את רדיוס ההתכנסות.
רדיוס תיאורטי[עריכת קוד מקור | עריכה]
ניתן למצוא את רדיוס ההתכנסות על ידי החלת מבחן השורש על תנאי הסדרה. מבחן השורש משתמש במספר
"lim sup" מציין את הגבול העליון . מבחן השורש קובע שהסדרה מתכנסת אם C < 1ומתבדר אם C > 1. מכאן נובע שסדרת החזקה מתכנסת אם המרחק מ- z למרכז a קטן מ
ומתבדר אם המרחק עולה על מספר זה; הצהרה זו היא משפט קאוצ'י-האמרד . שימו לב ש- r = 1/0 מתפרש כרדיוס אינסופי, כלומר f היא פונקציה שלמה .
הגבול הכרוך במבחן היחס הוא בדרך כלל קל יותר לחישוב, וכאשר הגבול הזה קיים, זה מראה שרדיוס ההתכנסות הוא סופי.
מבחן היחס אומר שהסדרה מתכנסת אם
זה שווה ערך ל
הערכה מעשית של רדיוס במקרה של מקדמים אמיתיים[עריכת קוד מקור | עריכה]
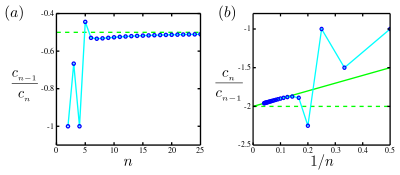
</br> הקו הירוק הרציף הוא אסימפטוטת הקו הישר בחלקת דומב-סייקס, [2] חלקה (b), המיירטת את הציר האנכי ב-2 ובעלת שיפוע +1. לפיכך יש ייחוד ב וכך הוא רדיוס ההתכנסות
בדרך כלל, ביישומים מדעיים, רק מספר סופי של מקדמי ידועים. בדרך כלל, כמו עולה, מקדמים אלה מתיצבים בהתנהגות קבועה שנקבעת על ידי הסינגולריות המגבילה את הרדיוס הקרובה ביותר. במקרה זה פותחו שתי טכניקות עיקריות, המבוססות על העובדה שהמקדמים של סדרת טיילור הם בערך אקספוננציאליים עם יחס כאשר r הוא רדיוס ההתכנסות.
- המקרה הבסיסי הוא כאשר המקדמים חולקים סימן משותף או סימן חלופי. במקרים רבים הגבול קיים, ובמקרה זה . שליליות פירוש הדבר שהסינגולריות המגבילה את ההתכנסות נמצאת על הציר השלילי. הערך את הגבול הזה, על ידי שרטוט של נגד , ואקסטרפולציה גרפית ל (ביעילות ) באמצעות התאמה ליניארית. פענוח עם מעריך את ההדדיות של רדיוס ההתכנסות, . שיטה זו נקראת דומב-סייקס . [3]
- המקרה המסובך יותר הוא כאשר לסימני המקדמים יש תבנית מורכבת יותר. מרסר ורוברטס הציעו את ההליך הבא. [4] הגדר את הרצף צייר את המספר הסופי של ידועים לעומת , והפקר גרפית באמצעות התאמה ליניארית. היירוט עם אומד את ההדדיות של רדיוס ההתכנסות, .
הערות[עריכת קוד מקור | עריכה]
- ^ Mathematical Analysis-II (באנגלית). Krishna Prakashan Media. 16 בנובמבר 2010.
{{cite book}}: (עזרה) - ^ See Figure 8.1 in: Hinch, E.J. (1991), Perturbation Methods, Cambridge Texts in Applied Mathematics, vol. 6, Cambridge University Press, p. 146, ISBN 0-521-37897-4
- ^ Domb, C.; Sykes, M.F. (1957), "On the susceptibility of a ferromagnetic above the Curie point", Proc. R. Soc. Lond. A, 240 (1221): 214–228, Bibcode:1957RSPSA.240..214D, doi:10.1098/rspa.1957.0078
- ^ Mercer, G.N.; Roberts, A.J. (1990), "A centre manifold description of contaminant dispersion in channels with varying flow properties", SIAM J. Appl. Math., 50 (6): 1547–1565, doi:10.1137/0150091
הפניות[עריכת קוד מקור | עריכה]
- Brown, James; Churchill, Ruel (1989), Complex variables and applications, New York: McGraw-Hill, ISBN 978-0-07-010905-6
- Stein, Elias; Shakarchi, Rami (2003), Complex Analysis, Princeton, New Jersey: Princeton University Press, ISBN 0-691-11385-8
ראו גם[עריכת קוד מקור | עריכה]
- משפט הבל
- מבחני התכנסות
- בדיקת שורש
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- רדיוס התכנסות, באתר MathWorld (באנגלית)








![{\displaystyle C=\limsup _{n\to \infty }{\sqrt[{n}]{|c_{n}(z-a)^{n}|}}=\limsup _{n\to \infty }\left({\sqrt[{n}]{|c_{n}|}}\right)|z-a|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c67486298c59df5fc7583a5cc253024ebc9045ea)
![{\displaystyle r={\frac {1}{\limsup _{n\to \infty }{\sqrt[{n}]{|c_{n}|}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb0428211dc308307cbbd69ed6151785382c549b)















