מושג המספר ביוון העתיקה

יוון העתיקה באזור המאה ה-5 לפנה"ס.

מספרים ביוון העתיקה היוו את הבסיס שממנו צמחה המתמטיקה כולה באותה העת.

המספר לא היה אמנם המצאה או תגלית של היוונים הקדמונים, שכן שימוש במספרים החל כבר בתרבויות הבבלית והמצרית, אך מתמטיקאים יוונים הציגו מגוון תפישות חדשניות למושג הזה.

מבוא

מתמטיקה ביוון העתיקה

ערך מורחב – מתמטיקה ביוון העתיקה

הגם שלא נמצאו כתבים מלאים רבים המתוארכים לפני שנת 30 לפנה"ס, המתעדים את ההיסטוריה של המתמטיקה בימי יוון הקדומה באופן סינכרוני, קיימות התייחסויות רבות למתמטיקה מהתקופה הקלאסית ועד לסוף התקופה ההלניסטית ובכתבים מאוחרים יותר.

ההתייחסות השלמה ביותר למתמטיקה היוונית העתיקה היא זו של פרוקלוס, בן המאה החמישית לספירה, שכתב פרשנות לספרו של אוקלידס, "יסודות", שנכתב בשנת 300 לפנה"ס לערך.

ציורו של אנטוניו צוקי מהמאה ה-18, פוטו יחד עם האנשה של המתמטיקה.

המתמטיקה ביוון העתיקה מהווה בסיס חשוב (גם אם לא בלעדי) למתמטיקה המודרנית. תכליתה נבדלת מזו שהייתה מקובלת בתרבויות המצרית והבבלית - שם התכלית הייתה פרקטית לצורכי חישוב, והיא דומה יותר (מכל מתמטיקה שקדמה לה), למתמטיקה הנלמדת באוניברסיטאות של ימינו, שבה גלומים רעיונות וגישות פורצי דרך שעקבותיהם ניכרים גם במתמטיקה המודרנית.

המתמטיקה היוונית הייתה בעלת מספר מאפיינים ייחודיים. הבולטים בהם היו:

• הוכחה - שימוש ברעיון ההוכחה ככלי לבחינת אמיתות טענות מתמטיות.
• אופי לא אמפירי - שימוש ברעיונות שאינם ניתנים בהכרח להוכחה בעזרת כלי שרטוט - למשל סרגל ומחוגה.
• הוכחה בדרך השלילה - פרקטיקה נפוצה בקרב מתמטיקאים, שאת העדות ההיסטורית הראשונה לה אנו מוצאים במתמטיקה ביוון העתיקה, בין היתר בגילוי מושג האינקרומנזביליות.

ישנן מספר בעיות מפורסמות, הידועות בשם "הבעיות הקלאסיות". בעיות אלו, לצד אחרות, הן עדות ליצירתיות ולייחודיות של המתמטיקה ביוון העתיקה, והן מדגימות את הבסיס לנושאים מתמטיים מתקדמים שאנחנו לומדים גם היום.

1. בעיית האינקומנזורביליות - הגילוי כי קיימים מספרים שאין להם "מידה משותפת", בניגוד לתפישה הרווחת באותה העת, לפיה כל המספרים יכולים להיות מבוטאים כיחס בין מספרים טבעיים - דבר שהוביל בהמשך הדרך לגילוי מספרים שאינם ניתנים לביטוי ביחס כזה - מספרים אי-רציונליים.
2. הכפלת הקובייה - "בהינתן מקצוע של קובייה, כיצד ניתן לבנות ממנה מקצוע של קובייה בעלת נפח כפול מהנפח המקורי".
3. ריבוע המעגל - או "תרבוע העיגול" - האם ניתן ליצור ריבוע השווה בשטחו לזה של מעגל בעזרת מספר סופי של צעדים.
4. חלוקת הזווית - או "שילוש הזווית" - כיצד ניתן לחלק זווית נתונה לשלושה חלקים שווים.

את הבעיות הללו ניסו מתמטיקאים יוונים לפתור בעזרת שימוש בסרגל ומחוגה, והן נחשבו לבעיות פתוחות עד המאה ה-19, שאז, בעזרת תורת גלואה, הצליחו להוכיח כי לא ניתן לפותרן באמצעות עזרים אלה.

הפיתגוראים ויחסם למספרים

הפיתגוראים.

פיתגורס, אחד מגדולי חכמי יוון בעת העתיקה, היה מתמטיקאי ופילוסוף ומייסד האסכולה הפיתגוראית שנקראה על שמו ופעלה באזור אסיה הקטנה בין המאה הששית לפנה"ס למאה הרביעית לפנה"ס.

הפיתגוראים היו קבוצה סגורה ופרטית אשר חבריה עברו מבחני קבלה, אשר שמרה על סודיות גדולה בקשר לעבודתה. הם פעלו כמסדר דתי ובית ספר פילוסופי ועסקו במתמטיקה, במוזיקה ובאסטרונומיה.

התעניינותם של הפיתגוראים במספרים הובילה אותם לחקור את תכונותיהם, כאשר את צעדיהם הראשונים עשו בחקר ההבדלים בין מספרים זוגיים לאי זוגיים. הם האמינו כי המספר הטבעי הוא יסודו של העולם. כלומר, המספר הוא אבן הבניין של כל הדברים, כך שלכל דבר קיים יש מספר המייצג אותו, ומכאן הסיקו שדבר שאינו ניתן לביטוי מתמטי שכזה אינו קיים.

גישה מתמטית-פילוסופית זו באה לדוגמה באפיון הקשר בין אורכי מיתרים לצלילים שהם מפיקים או בין מרחקים בין כוכבים, לבין נוסחאות מתמטיות שונות. כמו כן, היא מתבטאת גם בגילויו של פיתגורס כי הסולם המוזיקלי הוא מספר וניתן לתאר צלילים באמצעות שברים של מספרים שלמים.

המספר

ערך מורחב – ספרות יווניות

מספרים יוונים על קלף מהמאה הרביעית

בתקופת הפיתגוראים לא נעשה עדיין שימוש במערכת הספרתית שנמצאת בשימוש היום, ובפרט שימוש במניפולציות אלגבריות, במערכות של משוואות ובהגדרת פונקציות, אלא בעיקר הסתמכו על גאומטריה.

עם זאת, היוונים השתמשו בשיטה העשרונית המקובלת היום. במאה השישית לפנה"ס, הא"ב היווני הכיל 24 אותיות. אליהן התווספו שלושה סמלים נוספים, כך שייצגו את האחדות (1–9), העשרות (10–90) והמאות (100–900) באופן הבא:

אות	ערך	אות	ערך	אות	ערך
αʹ‎	1	ιʹ‎	10	ρʹ‎	100
βʹ‎	2	κʹ‎	20	σʹ‎	200
γʹ‎	3	λʹ‎	30	τʹ‎	300
δʹ‎	4	μʹ‎	40	υʹ‎	400
εʹ‎	5	νʹ‎	50	φʹ‎	500
ϛʹ‎	6	ξʹ‎	60	χʹ‎	600
ζʹ‎	7	οʹ‎	70	ψʹ‎	700
ηʹ‎	8	πʹ‎	80	ωʹ‎	800
θʹ‎	9	ϟʹ‎	90	ϡʹ‎	900

כך לדוגמה:

• MA הוא 41.
• PNE הוא 155.

סוגי מספרים ביוון עתיקה

השימוש במספרים ביוון העתיקה לא היה נפוץ כפי שהוא בתקופה המודרנית, ליוונים היו דרכים שונות לתאר מספרים. אחת מהן הייתה בנייה של צורות המתארות מספרים בעזרת אבנים, וכפי שנעשה במספרים ריבועיים, משולשים, מחומשים ומשושים.

מספרים פיתגוראים

פיתגורס ותלמידיו חשבו על המספרים הטבעיים כעל כללים שעל פיהם מתנהג העולם, ושדרכם אפשר ללמוד אותו ולהבינו. השקפתו של פיתגורס על מספרים באה לידי ביטוי גם בחיפוש תכונות מיוחדות, שלעיתים תוארו במונחים אסתטיים כ- "יפות" או "מכוערות", "מיוחדות" או "פשוטות". חלק מהתכונות הללו יכול לקבל תיאור מתמטי, כך לדוגמה מספר מושלם מוגדר כמספר השווה לסכום כל מחלקיו, לדוגמה $1+2+3=6$, או $14+7+4+2+1=28$, הם מספרים מושלמים.

סוג נוסף הוא מספרים המכונים מספרים ידידים. במתמטיקה, זוג מספרים הם ידידים אם כל אחד מהם שווה לסכום המחלקים של האחר. לדוגמה, זוג המספרים 220,284 הם מספרים ידידים, שכן: מחלקי המספר 220 הם 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 ו-110, וסכומם הוא 284. מחלקי המספר 284 הם 1, 2, 4, 71 ו-142, וסכומם הוא 220.

כפועל יוצא מדרכם של הפיתגוראים לתאר מספרים, בעיקר כסידורים שונים של אבנים, הם הגו מספר תיאוריות מוכרות שעסקו בתכונותיהם של מספרים. לדוגמה, תכונה בסיסית עבור מספרים זוגיים היא שניתן לייצגם בעזרתם שתי שורות זהות של אבנים, ובעבור מספרים אי-זוגיים, אם נייצגם בשתי שורות, תמיד תהיה שורה גדולה (או קטנה) באחת מהשנייה. משתי תכונות אלו הסיקו הפיתגוראים שסכום מספרים זוגיים תמיד יהיה זוגי, וכן סכום זוגי של מספרים אי זוגיים, יהיה תמיד זוגי גם הוא (מה שהיום מכונה מכפלה של מספר אי זוגי במספר זוגי). בעזרת סידורים אלו יצרו הפיתגוראים סוגים שונים של מספרים, וחקרו את הקשרים ביניהם.

מספרים ריבועיים

ערך מורחב – מספר ריבועי

מספרים ריבועיים

מספרים ריבועיים הם מספרים שכאשר מתארים אותם בעזרת סידור של אבנים, מקבלים ריבוע. כיום, אנו מתייחסים למספרים אלה כאל מספרים שלמים חיוביים שיכולים להיכתב כריבוע של מספר שלם אחר.

לדוגמה, עשרת המספרים הריבועיים הראשונים הם:

• $1=1^{2}$
• $4=2^{2}$
• $9=3^{2}$
• $16=4^{2}$
• $25=5^{2}$
• $36=6^{2}$
• $49=7^{2}$
• $64=8^{2}$
• $81=9^{2}$
• $100=10^{2}$

מספרים משולשים

ערך מורחב – מספר משולשי

מספרים משולשים

מספרים משולשים הם מספרים שייצוגם בעזרת סידור אבנים מוליד משולש שווה-צלעות. המספר המשולשי ה-nי שווה לסכום n המספרים הטבעיים הראשונים, המתקבל מחיבור סכום האיברים בשורה הראשונה, בשנייה, וכך הלאה עד קודקוד המשולש, שהוא 1.

המספרים המשולשים הראשונים הם 1, 3, 6, 10, 15, 21, 28, 36, 45.

על סמך התייחסות זו למספרים (כסידור של אבנים), טענו הפיתגוראים כי מספר ריבועי הוא סכום של שני מספרים משולשים עוקבים. לדוגמה: $10+6=16$ , וכאמור 16 הוא מספר ריבועי.

מספרים מוארכים

מספר מוארך

מספרים מוארכים הם מספרים שהם מכפלה של שני מספרים עוקבים. כלומר, מספרים מהצורה n(n+1) כאשר n הוא מספר טבעי. אלו מספרים שניתן לסדר כמלבן (מוארך, מכאן שמם) כך שההפרש בין צלעות המלבן יהיה 1.

דוגמה למספרים כאלו: 0, 2, 6, 12, 20, 30, 42, 56, 72, 90, 110, 132, 156, 182, 210, 240, 272, 306, 342, 380, 420, 462 …

הפיתגוראים הגדירו מספר מוארך גם בעזרת הגדרתם למספר המשולשי, כך שמספר מוארך שווה לפעמיים מספר משולשי. לדוגמה, $3+3=6$ או $15+15=30$. בדרך זו ניתן להמשיך וליצור גם מספרים מחומשים (היוצרים מחומש בסידור), ומשושים.

כהכללה, אפשר להתייחס לסוגים שונים של מספרים, בהתייחס לצורה שהם יוצרים, גם כמספרים מצולעים.

מספרים שבריים

היוונים עסקו רבות ביחסים ובפרופורציות בין מספרים. אמנם במרבית התייחסויותיהם ליחסים ולפרופורציות לא השתמשו המתמטיקאים היוונים במושג "שברים" כפי שאנו נוהגים לעשות היום, אך עדיין הציגו שימוש בשברים, בעיקר בטקסטים מעולמות העבודה הרלוונטיים להם או בהקשרים אסטרונומיים.

המספרים השבריים היווניים לא רק נבדלים מהשברים המקובלים במתמטיקה של ימינו מבחינת ההקשרים שבו היה נהוג להשתמש בהם, אלא גם מבחינה מהותית.

שימושים

יחסים ופרופורציה

תיאור של שברים כפי שאנחנו מכירים היום.

אחד מהמאפיינים המרכזיים של האריתמטיקה הפיתגוראית היה השימוש בפרופורציה, כלומר המצב שבו ארבעה מספרים, המסודרים בזוגות מייצגים את אותו היחס. לדוגמה, שני זוגות המספרים 2,3 ו-4,6 שמסודרים כך: 2/3 ו-4/6 נקראים "בעלי פרופורציה".

כיום נהוג להתייחס למספרים הללו כעל שברים ולערוך "צמצום" שלהם. הפיתגוראים לעומת זאת, הגדירו יחס כקשר, בהתייחס למידה של שני גדלים מאותו סוג. כלומר, ארבעה מספרים הם בפרופורציה אם הראשון והשני נמדדים לפי מידה מסוימת, והשלישי והרביעי עומדים באותו היחס בהתאמה לאותה המידה. עבור שני זוגות של גדלים, a,b ו-c,d. נאמר שזוגות אלה הם בעלי פרופורציה (או עומדים ביחס), אם קיימים שני מספרים שלמים, נסמנם m,n כך שמתקיים ש-n פעמים איזשהו מספר שלם כלשהו (נסמנו Ζ) הוא a ו-m פעמים Ζ הוא b, ובנוסף קיים מספר שלם אחר (נסמנו Τ), כך ש-n פעמים (אותו ה-n) Τ הוא c, וגם m פעמים (אותו ה-m) Τ הוא d. לדוגמה, עבור ${\frac {2}{3}}$ ו-${\frac {4}{6}}$ נקבל כי Ζ הוא 1 ו-Τ הוא 2.

כמו כן, אין אזכור לתיאור מובהק של פרופורציה בין מספרים אצל היוונים (לעומת קונבנציות אחרות מתקופת הרנסאנס שמסמנות a:b::c:d כדי לתאר פרופורציה בין a,b ל-c,d), והתיאור שלהם מילולי, כלומר "היחס בין a ל-b זהה ליחס בין c ל-d".

הגם שהיוונים השתמשו בפעולות חיבור חיסור וכפל במספרים, מבחינתם יחס היה דרך הנאותה להשוות בין מספרים ויחסים שיאפשרו להשוות בין סוגים שונים של יחס בלי לבצע פעולות על המספרים עצמם.

דוגמה לשוני בגישה של היוונים כלפי מושג היחס ובמסקנות שעלו מהן, בא לידי ביטוי במה שאנחנו מכירים היום כממוצע. אנחנו יודעים היום כי עבור שני מספרים, הממוצע שלהם הוא מספר שלישי שמקיים תנאי נוסף. הממוצע כפי שאנחנו מכירים אותו ("הממוצע החשבוני"), הוא מספר שלישי שנמצא במרחק שווה משני המספרים המקוריים. כלומר, בהינתן שני מספרים a ו-b, קיים מספר שלישי c המקיים $c-a=b-c$ (או, ביתר פירוט, $c={\frac {(a+b)}{2}}$).

המושג ממוצע הגיאומטרי מביע ביתר דיוק את ההתייחסות של היוונים למושג הפרופורציה. מבחינתם, הממוצע הגיאומטרי בין שני מספרים a,b היה מספר שלישי c, כך שהיחס בין a ל-c שווה ליחס בין c ל-b.

יחס הזהב

בעזרת הרעיונות של הפיתגוראים לגבי מושג הפרופורציה, נולד הרעיון המוכר לנו כיחס הזהב (המתמטיקאים ביוון העתיקה התייחסו אליו כ"mean and extreme ratio").

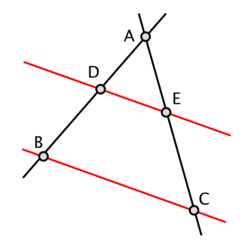
יחס הזהב מופיע בספרות המתמטית בהקשרים מגוונים, החל מסדרת פיבונאצ'י, דרך הופעתו בשלל תופעות טבע וביצירות אמנות ידועות במבנים מפורסמים, וכלה בתחום הסימטריה. ההקשר הבלעדי שהתייחסו אליו הפיתגוראים בכל הנוגע ליחס הזהב היה הפרופורציה. הם תיארו את יחס הזהב באופן הבא: "שתי עוצמות מתארות את יחס הזהב, אם היחס בין העוצמה הגדולה לקטנה שווה ליחס של סכומם לגדול מבניהם". ניתן לראות זאת בבירור בתמונה המופיעה לעיל.

יחס הזהב.

גילוי יחס הזהב אצל הפיתגוראים, התבסס, בין היתר, על החקירה של "הכוכב בעל חמשת הקודקודים", או הפנטגרם. גם בחקירה הזו, בדומה לחקירת הבעיות הקלאסיות של המתמטיקה היוונית, הם ניסו להבין האם ניתן לבנות צורה זו רק בעזרת סרגל ומחוגה. כלומר מדובר בבדיקה האם בניית פנטגרם אפשרית באמצעות היכולות לשרטט מעגל בהינתן רדיוס ומרכז, וכן למתוח קו ישר בין שתי נקודות - ותו לא. אחד מהגילויים המוקדמים של הפיתגוראים היה שיצירת צורה שכזו צריכה להתחיל משרטוט משולש שזוויות הבסיס שלו יהיו כפולות מהזווית השלישית (משולש ששתי זוויות הבסיס שלו שוות 72 מעלות וזווית הראש שלו שווה 36 מעלות). הם גילו שבשביל לקבל צורה כזו, עליהם לחלק ישר נתון לפי "יחס הזהב שלו".

העיסוק בשאלות אלו הוביל בין היתר לגילוי מושג האינקונמנזורביליות.

אינקונמנזורביליות

מספרים אי-רציונליים מפורסמים.

כאשר אנחנו מסתכלים לדוגמה על קטע מסוים, ניתן לחלק אותו למספר חלקים שאינם בהכרח שווים. אם ניתן לחלקו למספר חלקים, עולה השאלה מה היא המידה המשותפת האחידה שבעזרתה ניתן לחלק את הקטע.

האמונה עד אז של הפיתגוראים, הייתה שכל שני קטעים (או במונחים של ימינו - גדלים), ניתנים, כל אחד, לחלוקה למספר כלשהו של חלקים בעזרת מידה אחת משותפת כלשהי. מידה משותפת היא תכונה המאפשרת להשוות בין שני קטעים (או שני מספרים), לדוגמה a ו-b כך שקיים c שגם a וגם b ניתנים להרכבה ממספר שלם של עותקי c. במתמטיקה של ימינו, הכוונה היא שהיחס בין אורכי הקטעים הוא מספר רציונלי.

אם נחזור לבניית הפנטגרם של הפיתגוראים - בעזרתו הם הצליחו לגלות, ובהמשך גם להוכיח בניגוד לציפיותיהם, שעבור שני חלקים המקיימים את יחס הזהב - לא קיימת מידה משותפת ביניהם, מה שהוביל לגילוי "מידה אינקונמנזורבילית" או במתמטיקה של ימינו - מספרים אי רציונליים.

אם נשוב להגדרה של פרופורציה ויחס אצל הפיתגוראים אזי שבמצב כזה לא קיימים מספרים שלמים המקיימים את התכונה של פרופורציה.

דוגמה פשוטה לכך היא ריבוע היחידה - ריבוע שכל צלעותיו מאורך 1. ממשפט פיתגורס אנחנו יודעים שאורך האלכסון בריבוע כזה הוא שורש 2, כלומר לא קיימת מידה משותפת בין צלע הריבוע - 1, לבין אורך האלכסון שלו - ${\sqrt {2}}$.

כלומר, היוונים נתקלו במצב שבו בצורה הגיאומטרית הפשוטה ביותר קיימת בעיה שסתרה את כל מה שהאמינו בו עד אז - שמספרים טבעיים הם הדרך לתאר את כל הדברים ביקום, ושעל פיהם העולם פועל.

מעבר לאמונה זו שהתבררה כלא נכונה, היוונים נתקלו גם בבעיה טכנית. השימוש בפרופורציות היה אחד הכלים המרכזיים בעבודתם, אשר כפי שראינו הסתמך על כך שכל הגדלים מדידים בזוגות, טענה שכפועל יוצא - אף היא אינה נכונה.

באשר לעדויות ההיסטוריות, לא הרבה ידוע לנו על הנסיבות בהן הפיתגוראים הבינו את קיומם של גדלים אינקונמנזורביליים. קיימות עדויות מהן עולה שתובנות אלה נולדו בשנת 430 לפנה"ס לערך, כחלק מחקר הפנטגרם. הגם שנושא זה מצוי במחלוקת בין היסטוריונים, אין מחלוקת שגילוי גדלים אלו תרם רבות להתפתחות מושג המספר ביוון העתיקה ועד ימנו.

דוגמאות בולטות

השורש הריבועי של 2

האלכסון בריבוע היחידה.

כמתואר לעיל (אינקונמנזורביליות), לא הרבה ידוע על הדרך שבה הגיעו היוונים להוכחה זו. למרות זאת היסטוריונים רבים העלו השערות שונות כיצד נראתה הוכחה זו, ובפרט הוכחה המראה מדוע השורש הריבועי של 2 - הגודל של האלכסון בריבוע היחידה, הוא מספר אי רציונלי.

על מנת לתאר הוכחה זו, נציג תחילה את ההוכחה המודרנית לכך ששורש 2 הוא מספר אי-רציונלי. לשם כך נעשה שימוש בהוכחה על דרך השלילה:

נניח כי שורש 2 הוא אכן מספר רציונלי, כלומר ניתן לבטא את שורש 2 בעזרת שני מספרים טבעיים $p$ ו-$q$, כך ש:

${\sqrt {2}}={\frac {p}{q}}$. ניתן להניח כי ל-$p$ ול-$q$ אין מחלקים משותפים (שכן אחרת ניתן לצמצם אותם עד שנגיע למצב כזה). מכאן נובע ששני המספרים לא זוגיים (שכן אחרת 2 היה מחלק משותף של שניהם והיה אפשר להמשיך לצמצמם). כעת נעלה את שני אגפי המשוואה בריבוע ונקבל: $2={\frac {p^{2}}{q^{2}}}$. בעזרת פעולות אלגבריות פשוטות נקבל את המשוואה $p^{2}=2q^{2}$. לכן $p^{2}$ מספר זוגי, ובפרט $p$ זוגי. לכן, ניתן לבטא את $p$ באופן הבא: $p=2k$, כאשר $k$ מספר טבעי כלשהו. מהצבה במשוואה הקודמת, נקבל $4k^{2}=2q^{2}$, כלומר $q^{2}=2k^{2}$, ומאותו טיעון קודם, נקבל כי $q^{2}$ זוגי, ולכן גם $q$. בסה"כ נקבל כי גם $p$ וגם $q$ מספרים זוגיים, בסתירה להנחה שלנו, מה שמוביל לכך שההנחה שלנו כי שורש 2 הוא מספר רציונלי שגויה.

אם נחזור לפיתגוראים, העדות ההיסטורית להוכחה שלהם מופיעה בכתביו של אריסטו (prior Analytics Ι.23), שמתארת: "...האלכסון של ריבוע אינו בעל מידה משותפת לצלעו שכן אם נניח את קיומה של מידה משותפת, נקבל כי מספרים זוגיים שווים למספרים אי זוגיים - דבר המוביל לסתירה".

כלומר, אריסטו תיאר את ההוכחה של קיומן של מידות אינקונמנזורביליות כדוגמה להוכחה על דרך השלילה. לטענתו ההנחה היא שהאלכסון והצלע בריבוע הם בעלי מידה משותפת, ומתקבלת סתירה שאומרת שמספרים זוגיים שווים למספרים אי זוגיים. בספרו של אוקלידס, "יסודות", ובפרט בגרסה של תומאס הית', הוא מתאר גרסה מפורטת יותר של ההוכחה באופן הבא:

ריבוע ABCD.

נסתכל על ריבוע ABCD עם אלכסון BD. נניח שהאלכסון BD הוא בעל מידה משותפת עם הצלע BC. יהי $a:d$ היחס בין הצלע לאלכסון, בעזרת המספרים הקטנים ביותר האפשריים. כעת, $BC^{2}:BD^{2}=a^{2}:d^{2}$, וממשפט פיתגורס הקובע כי $BD^{2}=2BC^{2}$ נקבל כי $d^{2}=2a^{2}$. לכן נקבל כי $d^{2}$ זוגי ובפרט $d$ זוגי. מתוך ההנחה כי היחס $a:d$ מבוטא בעזרת המספרים הכי קטנים שניתן, נקבל כי $a$ חייב להיות אי זוגי. נסמן $d=2\gamma$, ולכן $4\gamma ^{2}=2a^{2}$, כלומר $a^{2}=2\gamma ^{2}$, ולכן $a^{2}$, כלומר $a$ זוגי. אבל $a$ הוא אי זוגי, ונקבל כי מספר זוגי שווה למספר אי זוגי - מה שלא ייתכן.

נשים לב שההוכחה המתוארת על ידי הית' דומה למדי להוכחה המודרנית שהצגנו קודם, אך כפי שאנו כבר יודעים לא בהכרח מדויקת היסטורית. איננו מכירים במתמטיקה היוונית שימוש בסימונים מתמטיים כמו משוואות, וכמו מעברים מסוג זה. לכן, ישנו הבדל היסטורי בין האופן שבו שאנחנו מתארים את שורש 2 כמספר אי רציונלי, לבין הטענה כי לא קיימת מידה משותפת בין צלע הריבוע לאלכסון שלו.

תאלס איש מילֵטוֹס

משפט תאלס הראשון.

תאלס היה פילוסוף יווני קדום ממילטוס באיוניה, ונחשב לראשון המתמטיקאים ביוון העתיקה.

בראייה היסטורית, תאלס פעל אומנם לפני פיתגורס והפיתגוראים, אך הוא ראוי להתייחסות, שכן הוא המתמטיקאי הראשון שמוזכר בכתביו של פרוקלוס. ישנן לא מעט עדויות היסטוריות על תאלס, אבל רובן נכתבו מאות שנים אחרי מותו, כמו חיזויו את ליקוי החמה ב-585 לפנה"ס ומדידת המרחק של ספינה מהחוף.

תאלס התעסק רבות בגיאומטריה, ומשפטי תאלס שאנחנו מכירים היום מיוחסים אליו. תאלס נחשב ככל הנראה למתמטיקאי הראשון שהוכיח משפט.

השפעות על המתמטיקה היום

לתפישת מושג המספר ביוון העתיקה הייתה השפעה גדולה על המתמטיקה בפרט, ועל האדם בכלל.השימוש בהוכחות מתמטיות, התייחסות למתמטיקה כנושא אקדמי, התפתחותה של המתמטיקה העיונית ורעיונות מתמטיים ופילוסופיים רבים נוספים, מקורם בתפישת המספר ביוון העתיקה.

לקריאה נוספת

• Leo Corry, A Brief History of Numbers, Oxford University Press, October 13, 2015
• Thomas L. Heath, The Thirteen Books of the Elements, Vol. 1-3 2nd ed. Edition, Dover publications inc. New York, 1956
• C. B. Boyer, A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach, 1989
• Victor J. Katz, A History of Mathematics: An Introduction, Pearson, 1993

הערות שוליים

בחינת הכניסה למכון המתמטיקה באוקראינה