למת הרגולריות של סמרדי

למת הרגולריות של סמרדי או בקיצור למת הרגולריות, היא משפט שימושי בקומבינטוריקה קיצונית שהתגלה על ידי המתמטיקאי ההונגרי אנדריי סמרדי (Endre Szemerédi). הלמה מאפשרת, בהינתן כל גרף (לא משנה כמה גדול הוא), לקרב אותו על ידי גרף בגודל קבוע, כשגודלו של הגרף המקרב נקבע רק על פי איכות הקירוב.

ללמה שימושים רבים, בקומבינטוריקה קיצונית ומחוץ לה, למשל במדעי המחשב. למרות חוזקה, הקבועים הגדולים שמעורבים בה הופכים אותה לתאורטית בלבד.

הלמה התגלתה על ידי סמרדי, תחילה כמקרה פרטי שעסק בגרפים דו צדדים, שהשתמש בה כדי להוכיח את משפט סמרדי בשנת 1975. המשפט אינו עוסק באופן ישיר בתורת הגרפים, אלא בקיומן של סדרות חשבוניות ארוכות כרצוננו בתתי קבוצות של מספרים טבעיים.

הלמה נוסחה והוכחה באופן מלא על ידו בשנת 1978.

הגדרות מקדימות

צפיפות

בקסידיתן גרף G, ושתי קבוצות קודקודים $X,Y\subseteq V$ נגדיר את הצפיפות ביניהן על ידי $d(X,Y)={\frac {|E(X,Y)|}{|X||Y|}}$ כאשר $E(X,Y)\ {\overset {\underset {\mathrm {def} }{}}{=}}\ \{(x,y):x\in X,y\in Y\}$

יש לציין שמספר זה אכן מציין (מנורמל במשקל של גודלי הקבוצות $X,Y$) את השאלה עד כמה "מלא" תת-הגרף של הקשתות בין $U$ ל $V$. אפשר לאמת שמספר זה שווה ל-1 אך ורק כאשר הגרף הוא מלא.

כמו כן, מספר זה מציין את ההסתברות שבהגרלת זוג קודקודים אקראי $(x,y)\in X\times Y$ בהתפלגות אחידה, יש ביניהם קשת בגרף.

זוג קבוצות רגולריות

נאמר שהקבוצות $X,Y$ הן $\varepsilon$ - רגולריות אם לכל שתי תתי קבוצות $A\subset X,B\subset Y$ המקיימות $|A|>\varepsilon |X|,|B|>\varepsilon |Y|$ מתקיים $|d(A,B)-d(X,Y)|<\varepsilon$.

כלומר, הצפיפות של כל שתי תתי קבוצות גדולות מספיק דומה לצפיפות של הקבוצות הגדולות. המשמעות האינטואיטיבית של זה היא שהקשתות בין X ל-Y מתפלגות "אחיד".

זוג קבוצות $\varepsilon$ רגולריותהצפיפות בתת-הקבוצות A,B דומה לצפיפות בין הקבוצות המקוריות. שימו לב ש A,B צריכות להיות גדולות יחסית - לפחות $\varepsilon$ כחלק יחסי מגודל הקבוצה המקורי

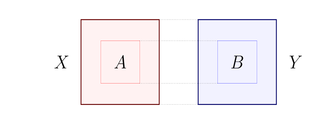
כדי להשתכנע בכך, אפשר לתאר לעצמנו מצב שבו מרבית הקשתות יוצאות ממספר קודקודים בודדים. במקרה זה, אם נשמיט "מעט" קודקודים (פחות מ $1-\varepsilon$ מגודל הקבוצה) עדיין נאבד את מרבית הקשתות. במצב זה זוג הקבוצות לא יהיה רגולרי.

חלוקה רגולרית של הגרף

תהא $V=\bigcup _{i=1}^{k}V_{i}$ חלוקה של צמתי הגרף לתתי קבוצות זרות זו לזו.

חלוקה של הגרף תקרא $\varepsilon$-רגולרית אם:

• כל הקבוצות בגודל שווה, כלומר קיים מספר $c\in \mathbb {N}$ כך ש $\forall _{i}|V_{i}|=c$, ובמלים אחרות $\forall _{i\neq j}|V_{i}|=|V_{j}|$
• מרבית הזוגות של מחלקות מתוך החלוקה הם רגולרים, וליתר דיוק - $V_{i},V_{j}$ הם זוג קבוצות $\varepsilon$ רגולריות - כמעט לכל $i,j$ - לכל הזוגות, למעט $\varepsilon k^{2}$ מתוך $k^{2}$ הזוגות האפשריים

כיוון שגודל הגרף לא תמיד מתחלק ב-k, התנאי הראשון לא תמיד מתקיים. ישנן שתי דרכים להתגבר על כך:

• להחליף את התנאי הראשון בתנאי $\forall _{i\neq j}||V_{i}|-|V_{j}||\leq 1$, כלומר כל הקבוצות כמעט שוות בגודלן (שונות בלכל היותר 1)
• להרשות קיום קבוצה נוספת (שמסמנים ב-$V_{0}$) שמקיימת $|V_{0}|<\varepsilon |V|=\varepsilon n$.

ניסוח הלמה

לכל $\varepsilon >0$ ולכל $m\in \mathbb {N}$ קיים $M=M(m,\varepsilon )$ כך שלכל גרף $G$ על לפחות $M$ קודקודים יש חלוקה $\varepsilon$ - רגולרית.

הלמה מבטיחה קיומה של חלוקה $\varepsilon$ - רגולרית בגרף בגודל גדול דיו (לכל $\varepsilon >0$) ועם לכל הפחות $m$ מחלקות. היות שהמבנה של חלוקה כזו נוח לעבודה ונותן מידע רב על הגרף, כוחה של הלמה הוא במתן מידע על מבנה הגרף אך ורק לפי מספר הקודקודים שלו.

רעיון ההוכחה

ההוכחה מתבססת על הגדרת פונקציה q שמקבלת חלוקה ומחזירה מספר בין 1 ל-0. הרעיון בהוכחה הוא להתחיל מהחלוקה הטריוויאלית לחלק אחד, וכל עוד היא לא ε-רגולרית, למצוא חלוקה שמעדנת אותה, כך ש-q גדלה. לשם כך, עבור כל זוג קבוצות שאינן רגולריות, מוצאים שתי תתי קבוצות שהצפיפות שלהן רחוקה מהצפיפות של הקבוצות הגדולות (קיומן של קבוצות כאלו נובע מהגדרת הרגולריות) ולקיחת החלוקה הגסה ביותר כך שכל אחת מתתי הקבוצות האלו יהיו איחוד מחלקות בחלוקה החדשה. אפשר להראות שערך ה-q גדל בלפחות ε⁵, ולפיכך תוך לכל היותר ε^-5 צעדים נגיע לחלוקה שהיא בהכרח רגולרית (כי ערך ה-q לא יכול לעלות מעבר ל-1).

בכל איטרציה, חילקנו את כל אחד מהחלקים למספר חלקים שעלול להיות אקספוננציאלי במספר הקודם (כי לכל חלק אחר מוצאים תת-קבוצה אחרת, והחלוקה שמעדנת את כולן עלולה להיות אקספוננציאלית). מכיוון שיש ε^-5 שלבים בהוכחה, מתקבל חסם שהוא tower-type של ε. בתחילה הייתה תקווה לשפר חסם זה, אך בשנת 1997 הוכיח טימותי גוורס חסם תחתון שגם הוא tower-type, ובכך ביטל תקווה זו.

שימושים

מהלמה אפשר לקבל גרף ממושקל שהוא "כיווץ" של הגרף המקורי: מחליפים כל קבוצת קודקודים בקודוקוד בודד, ובין כל שתי קבוצות שמים קשת שמשקלה כצפיפות בין שתי הקבוצות המקוריות. הגרף הזה מכיל את "כל המידע" על הגרף המקורי, ולפיכך פעולות שהיו קשות לעשייה על הגרף המקורי נהיות קלות יותר. אפשר למשל להוכיח שכדי לספור את מספר המשולשים בגרף G אפשר למצוא את הגרף המקרב G', לספור בו משולשים (כאשר "מספר המשולשים" בין שלושה קודקודים הוא מכפלת משקולות הקשתות) ואפשר להוכיח שהיחס בין מספר המשולשים ב-G' לגודלו קרוב (עד כדי ביטוי שתלוי ב-ε) ליחס הזה בגרף G.

graph removal lemma

ה-graph removal lemma (למת ההסרה) היא למה חשובה שניתן להוכיח באמצעות למת הרגולריות.

הלמה קובעת שבהינתן גרף H, בתנאים מסוימים (קיומו של עותק של H לאחר הסרת מעט קשתות מהגרף באופן יחסי) ניתן להבטיח את קיומם של עותקים רבים בגרף של H. באופן פורמלי:

יהי $G=(V,E)$ גרף על $n$ קודקודים ויהי H גרף על h קודקודים. נניח שקיים $\varepsilon >0$ כך שלכל הסרה של $\varepsilon n^{2}$ קשתות מן הגרף עדיין קיים שיכון של H בגרף. אז קיימת $\delta =\delta (h,\varepsilon )$ שתלויה רק ב-H וב-$\varepsilon$ (אבל לא ב-n) כך שהגרף מכיל לפחות $\delta \cdot n^{h}$ שיכונים זרים של H.

בדרך כלל מתייחסים לגרף H כאל "קבוע" ואך G כ"שואף לאינסוף". מקרה פרטי חשוב הוא כאשר H הוא משולש (מעגל מאורך 3) ואז הלמה נקראת triangle removal lemma (למת הסרת המשולשים).

הוכחת Graph Removal Lemma כיישום של הלמה של סמרדי

ההוכחה נחלקת למספר שלבים

1. הפעלת הלמה של סמרדי וקבלת חלוקה
2. הסרת חלק מן הקשתות הלא נוחות בגרף שהתקבל
3. שימוש ברגולריות הקבוצות על מנת להסיק קיומם של עותקים רבים של H בגרף שהתקבל (עותקים אלה היו קיימים, כמובן, גם בגרף המקורי).

יהא $G=(V,E)$ גרף, ויהי $\varepsilon _{0}>0$. על פי הלמה של סמרדי עבור $(\varepsilon ,m)=(\eta ,{\frac {1}{\eta }})$ כאשר $\eta ={\frac {\varepsilon _{0}}{5}}$, נקבל כי קיימת חלוקה $V=\bigcup _{i=0}^{r}V_{i}$ כפי שהוגדרה קודם לכן.

נסיר את הקשתות הבאות מן הגרף

• קשתות הסמוכות ל $V_{0}$. היות ש $|V_{0}|<\varepsilon n=$, קיימות לכל היותר $|V_{0}||V\setminus V_{0}|\leq |V_{0}||V|\leq \eta n^{2}$ קשתות שכאלה
• קשתות בין זוגות לא רגולריים $V_{i},V_{j}$. קיימים לכל היותר $\varepsilon \cdot r^{2}$ זוגות כאלה על פי הגדרת החלוקה, והיות ו $r\leq {\frac {n}{c}}$ מתקיים שקיימים לכל היותר $\eta n^{2}$ זוגות כאלה.
• קשתות פנימיות בתוך $V_{i}$. היות ש $|V_{i}|=c$ כמות הקשתות בתוך תת-הגרף $G|_{V_{i}}$ היא לכל היותר $|V_{i}|^{2}=c^{2}$ וישנם לכל היותר $r$ רכיבים כאלה, כך שכמות הקשתות הכוללת היא $r\cdot c^{2}\leq r\cdot {\frac {n^{2}}{m^{2}}}=r\cdot {\frac {n^{2}}{1/\eta ^{2}}}\leq r\cdot \eta ^{2}n^{2}$
• קשתות בין רכיבים עם צפיפות הנמוכה מ $d=2\eta$, כלומר הסרת כל הקשתות בין $V_{i},V_{j}$ המקיימים

$q(V_{i},V_{j})={\frac {|E(V_{i},V_{j})|}{|V_{i}||V_{j}|}}={\frac {|E(V_{i},V_{j})|}{c^{2}}}<d\iff |E(V_{i},V_{j})|<dc^{2}$

אם כן, כמות הקשתות שהסרנו בין רכיבים אלה היא לכל היותר - על פי התכונות של $n,r,c,d,\eta$ והקשרים ביניהם, בדומה למעברים קודם לכן -

$$\sum _{\underset {q(V_{i},V_{j})<d}{i,j=1}}^{r}|E(V_{i},V_{j})|<\sum _{\underset {q(V_{i},V_{j})<d}{i,j=1}}^{r}dc^{2}\leq \sum _{\underset {q(V_{i},V_{j})<d}{i,j=1}}^{r}d\left({\frac {n}{r}}\right)^{2}\leq \sum _{i,j=1}^{r}2\eta \left({\frac {n}{r}}\right)^{2}\leq dr^{2}\left({\frac {n}{r}}\right)^{2}\leq dn^{2}=2\eta n^{2}$$

כלומר סה"כ כמות הקשתות אותן הסרנו

$$\eta n^{2}+\eta n^{2}+rn^{2}\eta ^{2}+2\eta n^{2}\leq \varepsilon n^{2}$$

הקשתות שנותרו בגרף אם כן הן קשתות בין מחלקות שונות בצפיפות הגבוהה מ-d שהן גם זוג קבוצות $\varepsilon$ רגולריות

לאחר שמסכמים כל זאת, רואים שלא הסרנו יותר מאשר $\varepsilon n^{2}$ קשתות מן הגרף, מה שמבטיח לנו לפי ההנחה קיום של עותק של H בגרף שנותר. ניתן לשים לב שכל קודקוד של H צריך להיות במחלקה אחרת (שהרי לא השארנו קשתות שעוברות בין שני קודקודים באותה המחלקה). אם בין שני קודקודים של H (שנקרא להם x,y) הייתה קשת, אז בין המחלקות שהם שייכים אליהן הייתה לפחות קשת אחת. זה אומר שהצפיפות ביניהן היא לפחות d (שהרי כרגע בין כל שתי מחלקות הצפיפות היא או 0 או לפחות d, וראינו שהיא לא 0) והן גם רגולריות. להשלמת ההוכחה משתמשים ב-Graph Counting Lemma, שאומרת את הטענה הבאה:

יהי H גרף על הקודקודים $[h]=1,...,h$ עם s קשתות ויהיו $V_{1},...,V_{h}$ קבוצות קודקודים זרות כך שלכל $\{i,j\}\in E(H)$ מתקיים ש-$V_{i},V_{j}$ הן $\varepsilon$ רגולריות. אזי מספר העותקים של H בקודקודים הוא

$\left(\prod _{\{i,j\}\in E(H)}d(V_{i},V_{j})\right)\left(\prod _{i=1}^{k}|V_{i}|\right)\pm s\varepsilon \left(\prod _{i=1}^{k}|V_{i}|\right)$

כלומר, מספר העותקים קרוב למספר העותקים ה"צפוי" לפי צפיפויות הקשתות בין הקבוצות.

בעזרת למה זו ניתן להוכיח שקיימות לפחות $d^{s}\cdot \left({\frac {n}{k}}\right)^{h}$ עותקים של H ב-G. אם נסמן $\delta ={\frac {d^{s}}{k^{h}}}$ (נזכור ש-k,d,s,h לא תלויים ב-n), נקבל לפחות $\delta n^{h}$ עותקים של H כרצוי.

הכללות

ללמה יש הכללות רבות, רבות מהן נוגעות להיפרגרף, בדרך כלל k-יוניפורמי (כלומר, שכל קשת חלה בדיוק k קודקודים; גרף רגיל הוא 2 יוניפורמי). הכללות כאלו ניתנו על ידי גוורס, טרי טאו, נוגה אלון ועוד.

בכל ההכללות הללו, החסם המתקבל הוא תמיד השלב ה-k בהיררכית אקרמן (שלב 2 הוא מגדל חזקות).

הכללות נוספות נוגעות לשיפור הדיוק שהגרף המתקבל מקרב את הגרף המקורי.

קישורים חיצוניים

• Szemeredi's Regularity Lemma and its applications in graph theory