פונקציה עולה

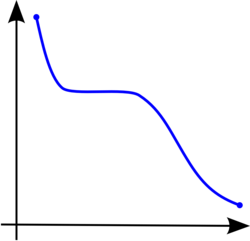
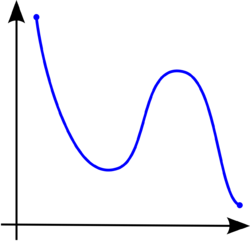
באנליזה מתמטית, פונקציה ממשית היא פונקציה עולה בקטע נתון, אם לכל בקטע מתקיים . בדומה, פונקציה יורדת היא כזו המקיימת לכל . אחת השאלות הבסיסיות בחקירה של פונקציה ממשית היא איתור התחומים שבהם היא עולה או יורדת.
פונקציות כאלה שכיחות בכל תחומי המדע: הקצב של תגובה כימית הוא פונקציה עולה של החום; תאוצת הנפילה של גוף היא פונקציה יורדת של המרחק מן הגוף אליו הוא נופל; ההיצע הוא פונקציה עולה של המחיר; כמות הנפט בכדור הארץ היא פונקציה יורדת של הזמן (מאז ראשית ההיסטוריה); ועוד.
פונקציות עולות ופונקציות יורדות הן סוגים מיוחדים של פונקציות מונוטוניות, ביחס לסדר הטבעי בישר הממשי.
הגדרות נוספות[עריכת קוד מקור | עריכה]
למונח "פונקציה עולה" יש, בהקשרים שונים, שני פירושים קרובים. אם לכל , אז הפונקציה עולה במובן החזק; אם מתקיים היחס החלש יותר לכל , אז הפונקציה עולה במובן החלש. באופן דומה מגדירים ירידה במובן החזק ובמובן החלש. פונקציה קבועה היא הפונקציה היחידה העולה ויורדת, במובן החלש, באותו קטע.
עליה וירידה אינם מושגים נקודתיים, משום שאת הערך בנקודה יחידה אין למה להשוות. עם זאת, אומרים שהפונקציה עולה בנקודה x אם קיים קטע פתוח המכיל את x, שבו הפונקציה עולה; וכן לפונקציה יורדת.
דוגמאות[עריכת קוד מקור | עריכה]
כל הדוגמאות הבאות הן של פונקציות ממשיות:
- הפונקציה היא עולה.
- הפונקציה היא יורדת.
- הפונקציה , כאשר קבוע, היא גם עולה וגם יורדת במובן החלש.
- פונקציית מדרגה היא עולה במובן החלש (אבל לא יורדת במובן החלש). פונקציה מהצורה הזו (שמקבלת ערכים קבועים על קטעים מסוימים) מכונה פונקציית מדרגות.
- הפונקציה בכללותה אינה מונוטונית, אך אם מסתכלים עליה רק בקטע היא עולה בו, ובקטע היא יורדת.
- בסעיף 121 לפקודת מס הכנסה[1] מוגדר גובה המס כפונקציה של השכר ברוטו. על הגדרה נאותה של פונקציה זו לקיים שני תנאים:
- גובה המס יהיה פונקציה עולה של גובה הברוטו (במילים פשוטות: על הכנסה גבוהה יותר חל מס גבוה יותר).
- גובה השכר נטו (שהוא השכר שנותר מהברוטו לאחר הפחתת המס) יהיה פונקציה עולה של גובה הברוטו (במילים פשוטות: מהכנסה גבוהה יותר נשאר נטו גבוה יותר).
דוגמה שאינה פונקציה ממשית:
- פונקציית מידה המוגדרת על אוסף קבוצות היא עולה חלש ביחס להכלה. כלומר אם אז .
- הפונקציה עולה (במובן החזק) בכל הישר הממשי.
- הפונקציה יורדת בכל הישר.
- הפונקציה עולה בקרן , ויורדת בקרן .
- פונקציית דיריכלה, המקבלת 1 בערכים רציונליים ו-0 בערכים אי רציונליים, אינה מונוטונית באף קטע.
מונוטוניות ורציפות[עריכת קוד מקור | עריכה]
אוסף נקודות אי הרציפות של פונקציה מונוטונית הן כולן "נקודות מסוג ראשון". קבוצות נקודות אי-הרציפות היא בת מנייה, הגם שאינה חייבת להיות סופית, ואף יכולה להיות צפופה אפילו כאשר הפונקציה חסומה, כפי שמראה הדוגמה הבאה:
- אם נסדר את המספרים הרציונליים בסדרה ונגדיר , אז הפונקציה עולה וחסומה, ואינה רציפה באף נקודה רציונלית.
מתכונות אלה של נקודות אי-הרציפות נובע שכל פונקציה מונוטונית המוגדרת בקטע סגור, היא אינטגרבילית לפי לבג.
לפונקציה מונוטונית במובן החזק, ורציפה, יש פונקציה הפכית שגם היא מונוטונית ורציפה.
את המונוטוניות אפשר לאבחן באמצעות הנגזרת, במקומות שבהם הפונקציה גזירה: אם פונקציה גזירה מונוטונית עולה בקטע מסוים נגזרתה אי-שלילית. אם היא מונוטונית יורדת, נגזרתה אינה חיובית. במסגרת מחקריו בתורת המידה, הוכיח אנרי לבג שפונקציה מונוטונית היא גזירה כמעט בכל מקום.
לפונקציה עולה מקטע סגור לעצמו יש (בדומה לפונקציה רציפה) נקודת שבת. המשפט אינו נכון עבור פונקציה יורדת.
מונוטוניות ונגזרות[עריכת קוד מקור | עריכה]
אם פונקציה f עולה במובן החלש בנקודה x, והיא גזירה שם, אז הנגזרת שלה מקיימת . מאידך, אם הפונקציה גזירה ו- , אז היא עולה, במובן החזק, בנקודה x:
- עולה במובן החלש ב-x עולה במובן החזק ב-x .
מבחינת ההתנהגות הנקודתית, העובדה ש- אינה מספיקה אפילו לעליה במובן החלש, כמו שמראה למשל הפונקציה בנקודה x=0. באופן דומה, אף אם הפונקציה עולה במובן החזק, זה אינו מבטיח שהנגזרת תהיה חיובית ממש, כפי שמדגימה הפונקציה .
כאשר מדובר בקטע פתוח, אם הפונקציה גזירה בכל הקטע והנגזרת שלה אי-שלילית, אז היא עולה שם במובן החלש. כך מתקבלים הקשרים
- עולה במובן החלש עולה במובן החזק .
במסגרת מחקריו בתורת המידה, הוכיח אנרי לבג שפונקציה מונוטונית היא גזירה כמעט בכל מקום.
ראו גם[עריכת קוד מקור | עריכה]
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ פקודת מס הכנסה, באתר חילן














![{\displaystyle \ (-\infty ,0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7a295f646a542a5c91ca8460e7a53ad3fbcd5da)












